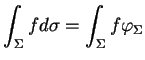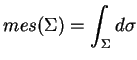


suivant: À propos de ce
monter: A..6 Densités et intégration
précédent: A..6.3 Cas des espaces
Table des matières
Sur une variété  plongée dans
plongée dans
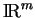 , de dimension
, de dimension 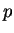 , une
, une 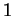 -densité est, à l'instar de ce qui se passe sur un espace affine, une fonction associant à chaque point
-densité est, à l'instar de ce qui se passe sur un espace affine, une fonction associant à chaque point 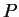 de
de 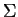 une densité de poids
une densité de poids 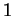 sur l'espace tangent
sur l'espace tangent 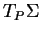 à
à 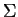 en ce point. Nous noterons
en ce point. Nous noterons
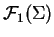 l'espace vectoriel de ces densités.
l'espace vectoriel de ces densités.
En la comparant au champ de 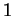 -densités
-densités
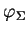 induit par le produit scalaire
induit par le produit scalaire 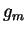 de
de
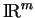 , on voit qu'une
, on voit qu'une 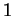 -densité
-densité 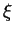 sur
sur 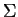 s'écrit d'une seule façon sous la forme
s'écrit d'une seule façon sous la forme
pour une certaine fonction
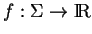 . L'espace
. L'espace
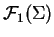 est ainsi canoniquement en bijection avec celui des foncions de
est ainsi canoniquement en bijection avec celui des foncions de 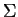 dans
dans
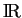 . Comme plus haut, on va utiliser cette fonction pour décider si
. Comme plus haut, on va utiliser cette fonction pour décider si 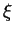 est intégrable et calculer son intégrale lorsqu'elle existe. Il y a une différence importante. Elle tient au fait qu'il n'y a généralement pas moyen de paramétrer globalement
est intégrable et calculer son intégrale lorsqu'elle existe. Il y a une différence importante. Elle tient au fait qu'il n'y a généralement pas moyen de paramétrer globalement 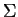 à un ensemble négligeable près. En fait, on recouvre
à un ensemble négligeable près. En fait, on recouvre 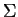 par des ouverts
par des ouverts
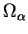 qui sont paramétrés par des applications
qui sont paramétrés par des applications
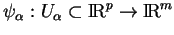 , on choisit une partition de l'unité
, on choisit une partition de l'unité
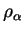 subordonnée à ce recouvrement (supposé localement fini dans le cas où il est dénombrable) et on pose
où
subordonnée à ce recouvrement (supposé localement fini dans le cas où il est dénombrable) et on pose
où 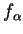 est l'expression de
est l'expression de
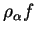 dans le paramétrage décrivant
dans le paramétrage décrivant
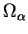 . Pour rappel,
est la valeur de
. Pour rappel,
est la valeur de
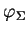 sur la base de l'espace tangent en
sur la base de l'espace tangent en
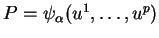 formée par les
formée par les
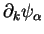 (voir (24)). Dans l'intégrale ci-dessus, l'intégrand est donc la valeur de
(voir (24)). Dans l'intégrale ci-dessus, l'intégrand est donc la valeur de
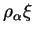 sur cette même base. L'indépendance aux différents choix de paramétrages est donc de nouveau une conséquence du comportement des densités sous l'effet d'un changement de base conjugué au théorème de changement de variables dans les intégrales. Il est facile de vérifier que l'expression est indépendante du choix de la partition de l'unité
sur cette même base. L'indépendance aux différents choix de paramétrages est donc de nouveau une conséquence du comportement des densités sous l'effet d'un changement de base conjugué au théorème de changement de variables dans les intégrales. Il est facile de vérifier que l'expression est indépendante du choix de la partition de l'unité
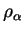 .
.
Lorsque 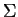 est un arc régulier de courbe décrit par une application surjective
est un arc régulier de courbe décrit par une application surjective
![$ \gamma:I=]a,b[\to\Sigma$](img1996.gif) , on suppose que
, on suppose que 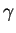 est de classe
est de classe 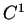 dans
dans 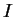 et que sa dérivée
et que sa dérivée 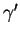 ne s'annule en aucun point de
ne s'annule en aucun point de 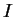 . Pour tout
. Pour tout 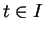 , c'est donc un paramétrage au voisinage de
, c'est donc un paramétrage au voisinage de 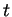 . En utilisant ces paramétrages dans la construction qu'on vient de décrire, on montre alors assez facilement que
. En utilisant ces paramétrages dans la construction qu'on vient de décrire, on montre alors assez facilement que
la dernière égalité étant vraie pour autant que 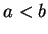 .
.
Naturellement, profitant de l'existence de
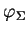 , on peut aussi introduire la notion de fonctions intégrables sur
, on peut aussi introduire la notion de fonctions intégrables sur 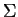 . Ce sont les fonctions
. Ce sont les fonctions
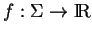 telles que
telles que
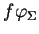 soit intégrable, l'intégrale d'une telle fonction étant alors
soit intégrable, l'intégrale d'une telle fonction étant alors
En particulier, on peut introduire la notion d'ensemblse intégrables, à savoir ceux dont la fonction caractéristique est intégrable. La mesure (le "volume") d'un tel ensemble est alors l'intégrale de sa fonction caractéristique. Pour autant qu'il soit intégrable, 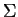 admet une mesure, donnée par
admet une mesure, donnée par

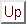


suivant: À propos de ce
monter: A..6 Densités et intégration
précédent: A..6.3 Cas des espaces
Table des matières
![]() -densités
-densités
![]() induit par le produit scalaire
induit par le produit scalaire ![]() de
de
![]() , on voit qu'une
, on voit qu'une ![]() -densité
-densité ![]() sur
sur ![]() s'écrit d'une seule façon sous la forme
s'écrit d'une seule façon sous la forme
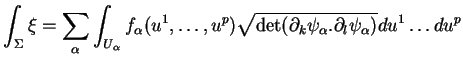
![]() est un arc régulier de courbe décrit par une application surjective
est un arc régulier de courbe décrit par une application surjective
![]() , on suppose que
, on suppose que ![]() est de classe
est de classe ![]() dans
dans ![]() et que sa dérivée
et que sa dérivée ![]() ne s'annule en aucun point de
ne s'annule en aucun point de ![]() . Pour tout
. Pour tout ![]() , c'est donc un paramétrage au voisinage de
, c'est donc un paramétrage au voisinage de ![]() . En utilisant ces paramétrages dans la construction qu'on vient de décrire, on montre alors assez facilement que
. En utilisant ces paramétrages dans la construction qu'on vient de décrire, on montre alors assez facilement que
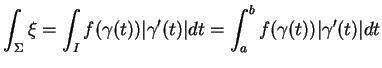
![]() , on peut aussi introduire la notion de fonctions intégrables sur
, on peut aussi introduire la notion de fonctions intégrables sur ![]() . Ce sont les fonctions
. Ce sont les fonctions
![]() telles que
telles que
![]() soit intégrable, l'intégrale d'une telle fonction étant alors
soit intégrable, l'intégrale d'une telle fonction étant alors