



suivant: A..6 Densités et intégration
monter: A..5 Densités et produits
précédent: A..5.1 Densités associées à
Table des matières
Considérons une variété plongée  dans
dans
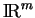 . Le produit scalaire
. Le produit scalaire 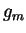 induit un produit scalaire
induit un produit scalaire 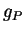 sur chaque espace tangent
sur chaque espace tangent
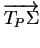 à
à  et définit ainsi un champ
et définit ainsi un champ
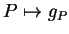 de produits scalaires sur
de produits scalaires sur  . Dans le cas des hypersurfaces, c'est la première forme fondamentale de
. Dans le cas des hypersurfaces, c'est la première forme fondamentale de  .
.
Il lui correspond un champ
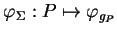 de
de  -densités sur
-densités sur  . Soit un paramétrage local arbitraire
. Soit un paramétrage local arbitraire 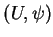 de
de  . Les dérivées partielles
. Les dérivées partielles
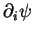 de
de 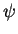 donnent une base (au sens classique) de l'espace tangent en
donnent une base (au sens classique) de l'espace tangent en
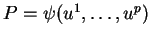 à laquelle correspond une base
à laquelle correspond une base
au sens utilisé dans ce texte. Avec la formule (23), on obtient alors l'expression de
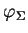 dans le paramétrage
dans le paramétrage 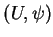
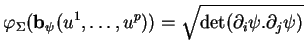 |
(A.4) |
(où le point "." indique le produit scalaire 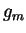 ). On reconnaît dans cette expression la formule usuelle donnant "l'élément de volume" de
). On reconnaît dans cette expression la formule usuelle donnant "l'élément de volume" de 
Considérons encore l'exemple d'un arc régulier de courbe 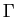 admettant le paramétrage local
admettant le paramétrage local
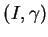 . La dérivée
. La dérivée 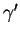 de
de 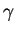 par rapport à
par rapport à 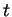 donne une base
donne une base
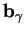 des vecteurs directeurs de la tangente à
des vecteurs directeurs de la tangente à 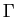 en
en 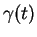 et induit donc une
et induit donc une  -densité
-densité
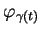 . Elle est calculée par la formule (23) qui donne
. Elle est calculée par la formule (23) qui donne
On retrouve ainsi l'élément de longueur
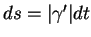 avec lequel on calcule les longueurs d'arc.
avec lequel on calcule les longueurs d'arc.
Nous allons bientôt comprendre en quoi les expressions telles que (24) ou 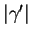 sont liées à des mesures de volume ou de longueur d'arc.
sont liées à des mesures de volume ou de longueur d'arc.




suivant: A..6 Densités et intégration
monter: A..5 Densités et produits
précédent: A..5.1 Densités associées à
Table des matières
![]() de
de ![]() -densités sur
-densités sur ![]() . Soit un paramétrage local arbitraire
. Soit un paramétrage local arbitraire ![]() de
de ![]() . Les dérivées partielles
. Les dérivées partielles
![]() de
de ![]() donnent une base (au sens classique) de l'espace tangent en
donnent une base (au sens classique) de l'espace tangent en
![]() à laquelle correspond une base
à laquelle correspond une base
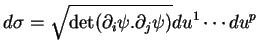
![]() admettant le paramétrage local
admettant le paramétrage local
![]() . La dérivée
. La dérivée ![]() de
de ![]() par rapport à
par rapport à ![]() donne une base
donne une base
![]() des vecteurs directeurs de la tangente à
des vecteurs directeurs de la tangente à ![]() en
en ![]() et induit donc une
et induit donc une ![]() -densité
-densité
![]() . Elle est calculée par la formule (23) qui donne
. Elle est calculée par la formule (23) qui donne
![]() sont liées à des mesures de volume ou de longueur d'arc.
sont liées à des mesures de volume ou de longueur d'arc.