



suivant: 7.2.2 Hyperplan d'appui
monter: 7.2 Quelques propriétés des
précédent: 7.2 Quelques propriétés des
Table des matières
La distance d'un point à un fermé est toujours réalisée. Dans le cas d'un ensemble convexe,
elle l'est de manière unique et le point en lequel elle est atteinte possède des propriétés intéressantes.
Rappelons qu'un sous-ensemble de
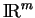 est convexe s'il contient les segments dont les extrémités lui appartiennent. Dans cette section, nous notons
est convexe s'il contient les segments dont les extrémités lui appartiennent. Dans cette section, nous notons  un convexe fermé de
un convexe fermé de
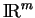 .
.
Proposition 58
Pour tout
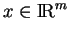
, la distance
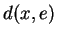
de
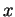
à

est réalisée en un point unique de

, la projection
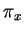
de
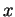
sur

.
Si
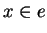
alors
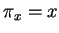
. Si
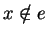
alors
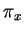
est un point frontière de

; c'est l'unique point
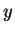
de

pour lequel l'hyperplan perpendiculaire à
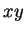
et passant par
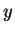
sépare
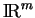
en deux demis-espaces dont l'un contient
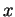
et l'autre

.
Si 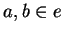 sont distincts et à égale distance de
sont distincts et à égale distance de 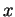 , alors le milieu du segment
, alors le milieu du segment ![$ [a,b]$](img1583.gif) est un point de
est un point de  plus proche de
plus proche de 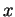 que chacun d'eux. La distance de
que chacun d'eux. La distance de 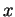 à
à  est donc réalisée en un point unique.
est donc réalisée en un point unique.
Supposons que 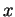 n'appartienne pas à
n'appartienne pas à  et donc que
et donc que
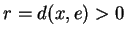 . Soit un point
. Soit un point  de
de  . Le segment
. Le segment ![$ [\pi_x,a]$](img1585.gif) est contenu dans
est contenu dans  . Il fait un angle au moins égal à
. Il fait un angle au moins égal à 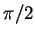 avec la demi-droite
avec la demi-droite 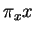 sans quoi il possèderait un point intérieur à la sphère de centre
sans quoi il possèderait un point intérieur à la sphère de centre 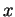 et de rayon
et de rayon 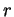 et qui serait donc plus proche de
et qui serait donc plus proche de 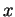 que
que 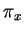 . Par conséquent, l'hyperplan tangent à cette sphère en
. Par conséquent, l'hyperplan tangent à cette sphère en 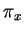 sépare
sépare  de
de 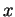 . Il est alors évident que
. Il est alors évident que 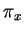 est dans la frontière de
est dans la frontière de  . Inversement, supposons que
. Inversement, supposons que 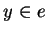 et que l'hyperplan perpendiculaire à
et que l'hyperplan perpendiculaire à 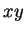 sépare
sépare  de
de 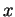 . Hormis
. Hormis 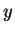 , les point de
, les point de  sont alors extérieurs à la sphère de centre
sont alors extérieurs à la sphère de centre 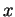 et de rayon
et de rayon 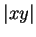 . Par conséquent
. Par conséquent 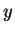 réalise la distance de
réalise la distance de 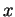 à
à  : c'est
: c'est 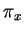 .
.
Proposition 59
Pour tout
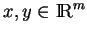
,
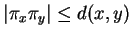
.
C'est évident si 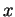 ou
ou 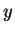 appartient à
appartient à  . Lorsqu'ils ne sont aucun dans
. Lorsqu'ils ne sont aucun dans  , la distance de
, la distance de 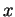 à la projection orthogonale
à la projection orthogonale 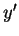 de
de 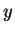 sur le plan
sur le plan
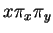 est moindre que celle de
est moindre que celle de 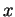 à
à 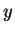 . Mais, dans ce plan, le segment
. Mais, dans ce plan, le segment
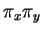 faisant des angles obtus avec les demi-droites
faisant des angles obtus avec les demi-droites 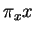 et
et 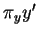 , il est clair que
, il est clair que
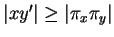 .
.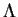




suivant: 7.2.2 Hyperplan d'appui
monter: 7.2 Quelques propriétés des
précédent: 7.2 Quelques propriétés des
Table des matières
![]() est convexe s'il contient les segments dont les extrémités lui appartiennent. Dans cette section, nous notons
est convexe s'il contient les segments dont les extrémités lui appartiennent. Dans cette section, nous notons ![]() un convexe fermé de
un convexe fermé de
![]() .
.
![]() n'appartienne pas à
n'appartienne pas à ![]() et donc que
et donc que
![]() . Soit un point
. Soit un point ![]() de
de ![]() . Le segment
. Le segment ![]() est contenu dans
est contenu dans ![]() . Il fait un angle au moins égal à
. Il fait un angle au moins égal à ![]() avec la demi-droite
avec la demi-droite ![]() sans quoi il possèderait un point intérieur à la sphère de centre
sans quoi il possèderait un point intérieur à la sphère de centre ![]() et de rayon
et de rayon ![]() et qui serait donc plus proche de
et qui serait donc plus proche de ![]() que
que ![]() . Par conséquent, l'hyperplan tangent à cette sphère en
. Par conséquent, l'hyperplan tangent à cette sphère en ![]() sépare
sépare ![]() de
de ![]() . Il est alors évident que
. Il est alors évident que ![]() est dans la frontière de
est dans la frontière de ![]() . Inversement, supposons que
. Inversement, supposons que ![]() et que l'hyperplan perpendiculaire à
et que l'hyperplan perpendiculaire à ![]() sépare
sépare ![]() de
de ![]() . Hormis
. Hormis ![]() , les point de
, les point de ![]() sont alors extérieurs à la sphère de centre
sont alors extérieurs à la sphère de centre ![]() et de rayon
et de rayon ![]() . Par conséquent
. Par conséquent ![]() réalise la distance de
réalise la distance de ![]() à
à ![]() : c'est
: c'est ![]() .
.![]()