Proposition 6.2.2
Le centre de l'algèbre de Poisson de
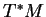
est l'ensemble des fonctions localement constantes. En particulier, si
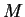
est connexe, ce sont exactement les constantes.
Preuve.
Nous allons voir que si
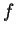
est dans le centre de l'algèbre de Poisson alors tout point
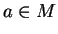
est contenu dans un ouvert
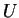
de
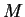
tel que
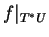
soit constant. En fait, il suffit de prendre pour
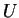
un domaine connexe de carte de
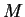
. En effet, les dérivées partielles de l'expression locale de
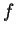
par rapport aux coordonnées canoniques correspondantes sont nulles puisque
Elle est donc constante si
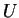
est connexe.
Par ailleurs, il est clair qu'une fonction localement constante est dans le centre de l'algèbre de Poisson.
Enfin, si
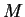
est connexe, les fonctions localement constantes sont constantes car l'ensemble des points en lesquels une telle fonction prend une valeur donnée est à la fois ouvert et fermé. S'il n'est pas vide, il coïncide donc avec
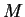
.
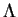
![\begin{displaymath}
% latex2html id marker 14857\begin{array}{rcl}
\{f,x^i\}&=...
...ex]
\{f,\xi_i\}&=&-\frac{\partial f}{\partial x^i}.
\end{array}\end{displaymath}](img1163.gif)