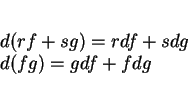
Nous pouvons à présent expliciter la base duale de la base
![]() associée à une carte
associée à une carte
![]() . On se souviendra en effet de ce que les composantes
. On se souviendra en effet de ce que les composantes ![]() de
de
![]() sont données par
sont données par
![]() , où
, où ![]() est le passage à la
est le passage à la ![]() -ème coordonnée locale. Autrement dit,
-ème coordonnée locale. Autrement dit,
![]() . La base duale cherchée est donc
. La base duale cherchée est donc
![]() . Ainsi, étant donnés
. Ainsi, étant donnés
![]() et
et
![]() , si
, si
![]() et
et
![]() , alors
, alors
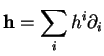 ,
, 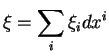
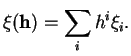
Les différentielles de fonctions sont des ![]() -formes particulières de
-formes particulières de ![]() , une
, une ![]() -forme
de
-forme
de ![]() étant une application
étant une application ![]() de classe
de classe ![]() de
de ![]() dans
dans ![]() telle que
telle que
![]() . On note
. On note
![]() l'ensemble de ces applications.
l'ensemble de ces applications.