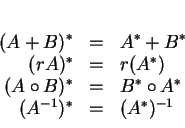


suivant: Bases duales
monter: 4.1 Rappels sur le
précédent: Dual d'un espace vectoriel
Table des matières
Toute application linéaire 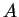 de
de 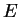 dans un espace vectoriel
dans un espace vectoriel 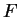 donne lieu à une application linéaire
donne lieu à une application linéaire 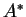 de
de 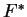 dans
dans 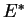 , la transposée de
, la transposée de 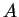 . Elle est définie par
Les propriétés suivantes sont faciles à vérifier.
. Elle est définie par
Les propriétés suivantes sont faciles à vérifier.
2003-11-02