1.2 Les axiomes

Un espace vectoriel (sur ${\rm I\!R}$) est un ensemble $E$ muni de deux opérations, l'addition

$$({\bf x},{\bf y}) \in E \times E \mapsto {\bf x}+{\bf y} \in E$$

et la multiplication scalaire

$$(\lambda,{\bf x}) \in {\rm I\!R}\times E \mapsto \lambda {\bf x} \in E,$$

astreintes à vérifier les propriétés suivantes, dans lesquelles ${\bf x}, {\bf y}, {\bf z}$ sont des éléments arbitraires de $E$ et $\lambda, \mu$ sont des nombres réels quelconques.

$$% latex2html id marker 27488\begin{array}{cl} {\bf (x+y) +... ...mu){\bf x}=\lambda(\mu{\bf x})\\ 1{\bf x}={\bf x} \end{array}$$

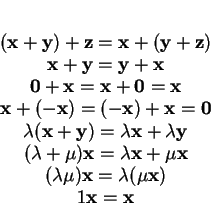
Dans la troisième, $\bf0$ est un élement particulier de $E$, l'élément neutre; dans la suivante, $-{\bf x}$ s'appelle l'opposé de ${\bf x}$.

Ces relations traduisent des règles de calcul familières de l'addition et du produit de nombres réels. On suppose ici qu'elles s'appliquent aussi aux éléments de $E$, sans préciser davantage la nature de ceux-ci. Voici d'autres propriétés usuelles satisfaites par les opérations dans $E$. Elles sont conséquences directes de ces règles.

Proposition 1.2.1  

$$% latex2html id marker 27503\begin{array}{c} Si \ {\bf x}+... ...f0}= {\bf0}\\ (-\lambda){\bf x}=-(\lambda{\bf x}) \end{array}$$

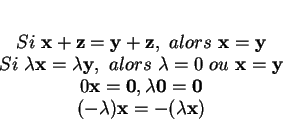
Les démonstrations sont omises. C'est un bon exercice que d'essayer d'en trouver. La dernière propriété justifie que l'on écrive $-\lambda {\bf x}$ pour $(-\lambda){\bf x}$ et ${\bf x}-{\bf y}$ pour ${\bf x}+(-{\bf y})$.