



suivant: 3.2.4 Complément orthogonal
monter: 3.2 Produit scalaire, longueur
précédent: 3.2.2.2 Angle de deux
Table des matières
Le fait que  soit muni d'un produit scalaire incite à privilégier les bases dans lesquelles l'expression de ce produit soit simple.
soit muni d'un produit scalaire incite à privilégier les bases dans lesquelles l'expression de ce produit soit simple.
Dans une base quelconque
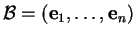 , à cause de la linéarité du produit par rapport à ses facteurs,
, à cause de la linéarité du produit par rapport à ses facteurs,
de sorte qu'il est déterminé par les produits
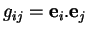 des éléments de
des éléments de
 .
Son expression est d'autant plus simple qu'un maximum de
.
Son expression est d'autant plus simple qu'un maximum de 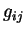 sont nuls.
On dit que
sont nuls.
On dit que
 est une base orthogonale si ses éléments sont deux à deux orthogonaux:
Elle est orthonormée si, de plus, ses éléments sont normés:
est une base orthogonale si ses éléments sont deux à deux orthogonaux:
Elle est orthonormée si, de plus, ses éléments sont normés:
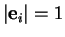 , pour tout
, pour tout 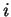 .
Dans ce cas, le passage aux composantes transforme le produit scalaire de
.
Dans ce cas, le passage aux composantes transforme le produit scalaire de  en celui de
en celui de
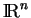 dont, bien entendu, la base canonique est orthonormée.
dont, bien entendu, la base canonique est orthonormée.
Nous admettrons sans le prouver que  admet des bases orthonormées.
(Ce n'est pas difficile à vérifier mais cela ne nous apporterait rien de significatif de le faire en détail.)
admet des bases orthonormées.
(Ce n'est pas difficile à vérifier mais cela ne nous apporterait rien de significatif de le faire en détail.)
Remarque 3.2.3
La matrice exprimant le changement de coordonnées résultant d'un changement de bases orthonormées de

est orthogonale. Ses colonnes
sont en effet formées des composantes des vecteurs de l'une d'elles exprimés dans l'autre (cf. Remarque
4.7). En particulier, le déterminant de cette
matrice est
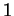
ou
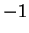
.
Proposition 3.2.4
Des vecteurs
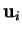
non nuls et orthogonaux deux à deux sont linéairement indépendants.
Preuve. Le produit scalaire de la relation
par 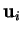 donne
donne
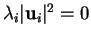 . Puisque
. Puisque 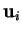 n'est pas nul, cela implique
n'est pas nul, cela implique
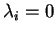 .
.
Les composantes 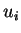 de
de 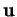 dans une base orthonormée
dans une base orthonormée
 sont données par
sont données par
Ce sont donc les mesures algébriques des projections orthogonales de 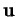 sur les
sur les 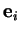 . En particulier, si
. En particulier, si 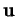 est normé, alors il est donné par ses cosinus directeurs
où
est normé, alors il est donné par ses cosinus directeurs
où 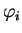 est l'angle qu'il fait avec
est l'angle qu'il fait avec 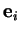 .
.




suivant: 3.2.4 Complément orthogonal
monter: 3.2 Produit scalaire, longueur
précédent: 3.2.2.2 Angle de deux
Table des matières
2002-12-17
![]() soit muni d'un produit scalaire incite à privilégier les bases dans lesquelles l'expression de ce produit soit simple.
soit muni d'un produit scalaire incite à privilégier les bases dans lesquelles l'expression de ce produit soit simple.
![]() , à cause de la linéarité du produit par rapport à ses facteurs,
, à cause de la linéarité du produit par rapport à ses facteurs,
![]() admet des bases orthonormées.
(Ce n'est pas difficile à vérifier mais cela ne nous apporterait rien de significatif de le faire en détail.)
admet des bases orthonormées.
(Ce n'est pas difficile à vérifier mais cela ne nous apporterait rien de significatif de le faire en détail.)
![]() de
de ![]() dans une base orthonormée
dans une base orthonormée
![]() sont données par
sont données par