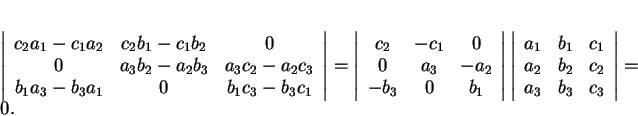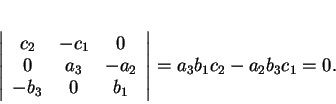suivant: 2.8.2 Formulation classique
monter: 2.8 Le théorème de
précédent: 2.8 Le théorème de
Table des matières
Théorème 2.8.1
Soient des droites
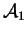
,
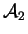
,
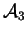
,
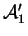
,
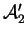
et
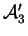
qui se coupent en un même point.
On suppose que trois quelconques de ces droites ne sont jamais coplanaires.
Les plans
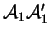
,
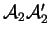
et
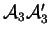
ont une droite en commun si et seulement si les droites
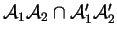
,
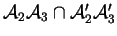
et
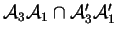
sont coplanaires.
Preuve. Prenons un repère dont l'origine soit le point commun aux six droites et dont la base
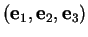 soit formée de vecteurs-directeurs de
soit formée de vecteurs-directeurs de
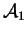 ,
,
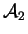 et
et
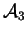 respectivement (ces droites n'étant pas coplanaires, des vecteurs-directeurs choisis sur chacune sont d'office linéairement
indépendants). Notons
respectivement (ces droites n'étant pas coplanaires, des vecteurs-directeurs choisis sur chacune sont d'office linéairement
indépendants). Notons
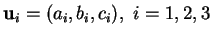 , les composantes de vecteurs-directeurs de
, les composantes de vecteurs-directeurs de
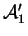 ,
,
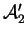 et
et
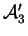 . Les
. Les 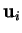 sont linéairement
indépendants (puisque les droites en question ne sont pas coplanaires). De plus, aucune de leurs composantes n'est nulle car sinon, l'un des
sont linéairement
indépendants (puisque les droites en question ne sont pas coplanaires). De plus, aucune de leurs composantes n'est nulle car sinon, l'un des
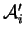 serait dans le
plan formé par deux des
serait dans le
plan formé par deux des
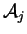 .
.
Les plans
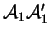 ,
,
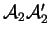 et
et
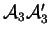 admettent respectivement les équations cartésiennes (on note
admettent respectivement les équations cartésiennes (on note 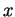 ,
, 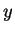 ,
, 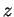 les coordonnées d'un point
quelconque):
les coordonnées d'un point
quelconque):
Ils ont une droite en commun si et seulement si
En effet, par le Corollaire 5.14, ceci exprime le fait que leurs sous-vectoriels directeurs ont une droite vectorielle en commun, ce qui suffit puisqu'ils
passent déjà par un même point.
Par ailleurs,
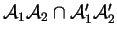 possède le vecteur-directeur de composantes
possède le vecteur-directeur de composantes
Pour
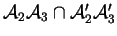 et
et
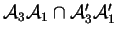 , on obtient semblablement
, on obtient semblablement
et
Les trois droites sont donc coplanaires si et seulement si
Puisque les 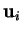 sont linéairement indépendants,
n'est pas nul et la condition revient donc à
D'où la conclusion.
sont linéairement indépendants,
n'est pas nul et la condition revient donc à
D'où la conclusion.




suivant: 2.8.2 Formulation classique
monter: 2.8 Le théorème de
précédent: 2.8 Le théorème de
Table des matières
2002-12-17
![]() ,
,
![]() et
et
![]() admettent respectivement les équations cartésiennes (on note
admettent respectivement les équations cartésiennes (on note ![]() ,
, ![]() ,
, ![]() les coordonnées d'un point
quelconque):
les coordonnées d'un point
quelconque):
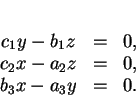
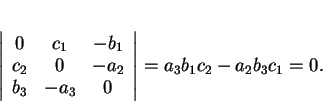
![]() possède le vecteur-directeur de composantes
possède le vecteur-directeur de composantes