2.3.1 Combinaisons affines

Il y a deux cas où l'on peut donner un sens à l'expression

$$\alpha_1A_1+ \cdots +\alpha_pA_p$$ (2.1)

où $\alpha_1, \ldots ,\alpha_p$ sont des nombres et $A_1, \ldots ,A_p$ des points.

Lemme 2.3.1   Soit $S\in {\mathcal E}$.

(i) Si $\alpha_1+ \cdots +\alpha_p=0$ alors l'élément

$$\alpha_1\overrightarrow{SA_1}+ \cdots +\alpha_p\overrightarrow{SA_p}$$

de $E$ ne dépend pas de $S$.

(ii) Si $\alpha_1+ \cdots +\alpha_p=1$ alors le point

$$S+\alpha_1\overrightarrow{SA_1}+ \cdots +\alpha_p\overrightarrow{SA_p}$$

de ${\mathcal E}$ ne dépend pas de $S$.

Preuve. Soit $S'\in {\mathcal E}$. On a

$$\alpha_1\overrightarrow{S'A_1}+ \cdots +\alpha_p\overrightarrow{S'A_p} = \alpha_1(\overrightarrow{S'S}+\overrightarrow{SA_1})+ \cdots +\alpha_p(\overrightarrow{S'S}+\overrightarrow{SA_p})$$

$$= (\alpha_1+ \cdots +\alpha_p)\overrightarrow{S'S}+\alpha_1\overrightarrow{SA_1}+ \cdots +\alpha_p\overrightarrow{SA_p}.$$

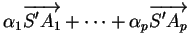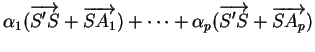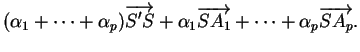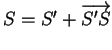On en déduit immédiatement (i). En ajoutant $S'$ aux membres de ces égalités, et en utilisant $S=S'+\overrightarrow{S'S}$, on en déduit aussi (ii).$\qed$

Par convention, (9) représente le vecteur ou le point obtenu en (i) ou en (ii) quand $\alpha_1+ \cdots +\alpha_p$ vaut 0 ou $1$ respectivement. Dans le premier cas, ceci généralise la notation $Y-X$ désignant $\overrightarrow{XY}$. Dans le second cas, on dit que (9) est une combinaison affine de $A_1, \ldots ,A_p$, ou leur barycentre pour les poids $\alpha_1, \ldots ,\alpha_p$. Lorsque les poids sont égaux, on l'appelle aussi centre de gravité.

Le centre de masse de points matériels $P_i$ est une combinaison affine de ceux-ci dont les coeficients $\alpha_i=\frac{m_i}{m}$ sont tous positifs.

Quand $p=2$, $\alpha_1=1-\alpha_2$ et on écrit souvent la combinaison affine $\alpha_1A_1+\alpha_2A_2$ sous la forme $(1-\lambda) A_1+\lambda A_2$.