



suivant: 7.7.0.1.2 Conclusions
monter: 7.7.0.1 Réduction et classification
précédent: 7.7.0.1 Réduction et classification
Table des matières
Comme en dimension 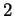 (cf. (4.3)), l'équation la plus générale du second degré en
(cf. (4.3)), l'équation la plus générale du second degré en
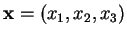 s'écrit sous la forme
où
s'écrit sous la forme
où 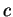 un nombre,
un nombre, 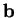 un élément de
un élément de
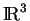 et
et  est une matrice symétrique,
carrée de dimension
est une matrice symétrique,
carrée de dimension 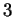 , non nulle. Elle est donc diagonalisable par
une matrice que l'on peut choisir orthogonale et de déterminant
, non nulle. Elle est donc diagonalisable par
une matrice que l'on peut choisir orthogonale et de déterminant 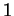 si
on le souhaite. Ceci permet, comme dans le cas des courbes du second
degré, de trouver un repère dans lequel l'équation s'écrit
Les remarques a) et b) que l'on a faites à l'occasion de la
discussion des équations à deux variables (4.3) s'appliquent ici.
On peut en ajouter une qui n'était pas pertinente à cet endroit:
si
on le souhaite. Ceci permet, comme dans le cas des courbes du second
degré, de trouver un repère dans lequel l'équation s'écrit
Les remarques a) et b) que l'on a faites à l'occasion de la
discussion des équations à deux variables (4.3) s'appliquent ici.
On peut en ajouter une qui n'était pas pertinente à cet endroit:
c)Si un des 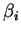 n'est pas nul, alors on peut supposer
qu'il n'y en a qu'un.
n'est pas nul, alors on peut supposer
qu'il n'y en a qu'un.
En effet, il suffit de remplacer 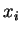 par la somme
par la somme 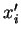 des
termes du premier degré figurant dans l'équation.
des
termes du premier degré figurant dans l'équation.
2002-12-17
![]() n'est pas nul, alors on peut supposer
qu'il n'y en a qu'un.
n'est pas nul, alors on peut supposer
qu'il n'y en a qu'un.
![]() par la somme
par la somme ![]() des
termes du premier degré figurant dans l'équation.
des
termes du premier degré figurant dans l'équation.