



suivant: 6.2.2.1 Cas d'un seul
monter: 6.2 Continuité, dérivabilité, etc.
précédent: 6.2.1 Gradient d'une fonction
Table des matières
Soit une fonction
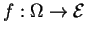 , où
, où 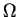 est un ouvert de
est un ouvert de
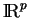 .
Les composantes de
.
Les composantes de 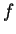 dans un repère
dans un repère
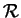 sont des fonctions ordinaires
sont des fonctions ordinaires
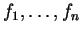 en les arguments
en les arguments
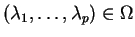 de
de 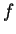 .
Nous dirons que
.
Nous dirons que 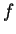 est continu, dérivable, etc. dans
est continu, dérivable, etc. dans 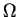 si ces fonctions le sont au sens usuel de l'analyse.
Il s'agit de nouveau de propriétés indépendantes du repère, car lors d'un changement de repère, les nouvelles composantes de
si ces fonctions le sont au sens usuel de l'analyse.
Il s'agit de nouveau de propriétés indépendantes du repère, car lors d'un changement de repère, les nouvelles composantes de 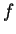 sont des combinaisons linéaires
des anciennes. Elles possèdent donc les mêmes propriétés analytiques que celles-ci.
sont des combinaisons linéaires
des anciennes. Elles possèdent donc les mêmes propriétés analytiques que celles-ci.
Les dérivées de 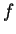 ont une interprétation géométrique utile: ce sont des éléments de
ont une interprétation géométrique utile: ce sont des éléments de
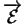 .
Expliquons cela à propos de la dérivée de
.
Expliquons cela à propos de la dérivée de 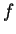 dans une direction
dans une direction
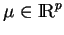 en un point
en un point
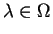 .
Lorsque l'argument de
.
Lorsque l'argument de 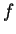 passe de
passe de 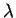 à
à
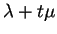 , l'image de
, l'image de 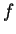 subit une translation de vecteur
subit une translation de vecteur
Le quotient
dont la limite est la dérivée éventuelle de 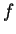 est donc un élément de
est donc un élément de
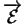 qui représente en quelque sorte la translation moyenne résultant du
changement d'argument. Voici comment on peut calculer pratiquement cette dérivée. Ci-dessous,
qui représente en quelque sorte la translation moyenne résultant du
changement d'argument. Voici comment on peut calculer pratiquement cette dérivée. Ci-dessous,
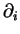 représente la dérivée partielle par rapport à la
variable de numéro
représente la dérivée partielle par rapport à la
variable de numéro 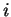 , convention que nous utiliserons régulièrement par la suite.
, convention que nous utiliserons régulièrement par la suite.
Proposition 6.2.4
Soient une fonction
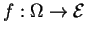
de classe
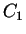
, où
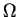
est un ouvert de
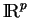
et
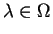
.
La limite
existe pour chaque
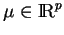
. Elle dépend linéairement de
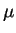
. Ses composantes dans un repère arbitraire de
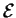
sont données matriciellement par
où les
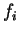
sont les composantes de
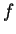
dans le repère.
La preuve est analogue à celle de la propriété précédente. Nous ne la détaillerons pas.
On désigne aussi
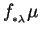 par
par
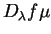 . Quand
. Quand 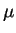 est un des vecteurs
est un des vecteurs
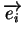 de la base canonique de
de la base canonique de
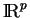 , il n'y a pas
d'inconvénient à le désigner comme une dérivée partielle, c'est-à-dire par
, il n'y a pas
d'inconvénient à le désigner comme une dérivée partielle, c'est-à-dire par
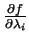 , voire par
, voire par
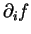 .
.
Sous-sections




suivant: 6.2.2.1 Cas d'un seul
monter: 6.2 Continuité, dérivabilité, etc.
précédent: 6.2.1 Gradient d'une fonction
Table des matières
2002-12-17
![]() ont une interprétation géométrique utile: ce sont des éléments de
ont une interprétation géométrique utile: ce sont des éléments de
![]() .
Expliquons cela à propos de la dérivée de
.
Expliquons cela à propos de la dérivée de ![]() dans une direction
dans une direction
![]() en un point
en un point
![]() .
Lorsque l'argument de
.
Lorsque l'argument de ![]() passe de
passe de ![]() à
à
![]() , l'image de
, l'image de ![]() subit une translation de vecteur
subit une translation de vecteur
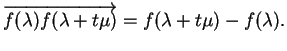
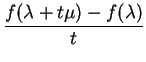
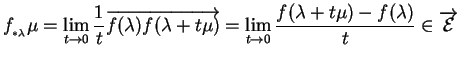
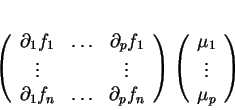
![]() par
par
![]() . Quand
. Quand ![]() est un des vecteurs
est un des vecteurs
![]() de la base canonique de
de la base canonique de
![]() , il n'y a pas
d'inconvénient à le désigner comme une dérivée partielle, c'est-à-dire par
, il n'y a pas
d'inconvénient à le désigner comme une dérivée partielle, c'est-à-dire par
![]() , voire par
, voire par
![]() .
.