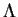next up previous contents
suivant: 6.2.3 Le théorème de monter: 6.2 La seconde forme précédent: 6.2.1 Normale   Table des matières

6.2.2 Equations de structure (II)

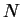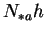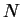Comme la longueur de $ N$ est constante, les dérivées $ N_{*a}h$ de $ N$ lui sont perpendiculaires. Elles sont donc tangentes à $ \Sigma$ en $ a$. L'application

$\displaystyle W_a:h\in\overrightarrow{T_a\Sigma}\mapsto N_{*a}h\in\overrightarrow{T_a\Sigma} $

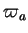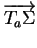est l'application de Weingarten de $ \Sigma$ en $ a$. La seconde forme fondamentale $ \varpi_a$ de $ \Sigma$ en $ a$ est la forme bilinéaire de $ \overrightarrow{T_a\Sigma}$ définie par

$\displaystyle \varpi_a(h,k)=-g(W_a(h),k). $

Elle permet de compléter les équations de structure donnée plus haut.

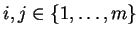
Proposition 49   Pour tous $ i,j\in\{1,\ldots,m\}$, on a

$\displaystyle \partial_{ij}\varphi.N=\varpi(\partial_i\varphi,\partial_j\varphi). $

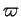
En particulier, $ \varpi$ est symmétrique.

On a en effet

$\displaystyle \partial_{ij}\varphi.N=\partial_i(\partial_j\varphi.N)-\partial_j\varphi.\partial_iN=-\partial_j\varphi.\partial_iN $

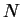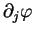car $ N$ est perpendiculaire à $ \partial_j\varphi$.$ \qedsymbol$