La vérification est directe. Elle repose essentiellement sur les formules
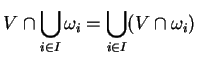
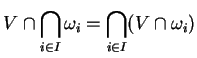
Le lecteur aurait intérêt à vérifier ce fait par lui-même. De tels petits exercices sont bien utiles lors des premièrs contact avec une discipline aussi abstraite que la topologie.
Dans ce texte, sauf mention explicite du contraire, toute partie
![]() sera considérée comme munie de la topologie induite par la topologie classique de
sera considérée comme munie de la topologie induite par la topologie classique de
![]() . Lorsqu'il sera nécessaire de la mentionner explicitement, nous noterons
. Lorsqu'il sera nécessaire de la mentionner explicitement, nous noterons ![]() cette topologie induite.
cette topologie induite.