



suivant: 3.2.5 Le groupe des
monter: 3.2 Groupes de matrices
précédent: 3.2.3 Le groupe unimodulaire
Table des matières
On note 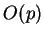 le sous-groupe de
le sous-groupe de
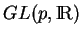 formé des matrices orthogonales. C'est le groupe des
isométries (ayant 0 comme
point fixe) de
formé des matrices orthogonales. C'est le groupe des
isométries (ayant 0 comme
point fixe) de
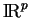 . L'application
. L'application
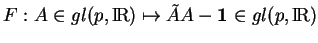 prend ses valeurs
dans l'espace
prend ses valeurs
dans l'espace
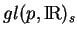 des matrices
symétriques. Son application linéaire tangente en
des matrices
symétriques. Son application linéaire tangente en 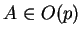 est
donnée par
Son noyau est donc formé des matrices
est
donnée par
Son noyau est donc formé des matrices 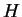 pour lesquelles
pour lesquelles 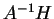 est antisymétrique. Comme
est antisymétrique. Comme
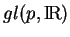 est la somme directe de
est la somme directe de
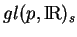 et de l'espace
et de l'espace
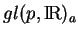 des matrices antisymétriques, lorsque
des matrices antisymétriques, lorsque 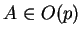 , le
rang de
, le
rang de 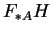 est donc
est donc
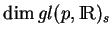 . Par conséquent,
. Par conséquent,
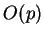 est une variété
plongée de dimension
est une variété
plongée de dimension
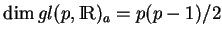 dans
dans
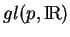 .
.