



suivant: A..4.2 L'application
monter: A..4 Produits scalaires
précédent: A..4 Produits scalaires
Table des matières
Dans ce texte, nous allons noter
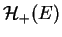 l'ensemble des produits scalaires de
l'ensemble des produits scalaires de  . Le groupe
. Le groupe 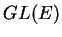 des bijections linéaires de
des bijections linéaires de  dans lui-même opère sur cet espace, par l'action
dans lui-même opère sur cet espace, par l'action
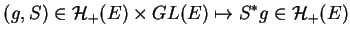 |
(A.2) |
Plus généralement, toute bijection linéaire
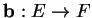 entre espaces vectoriels de dimension finie induit une bijection
Elle est donnée par
On a
En particulier, l'action (22) est une action à droite.
entre espaces vectoriels de dimension finie induit une bijection
Elle est donnée par
On a
En particulier, l'action (22) est une action à droite.
Proposition 71
L'action de
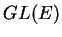
sur
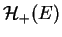
est transitive
Ceci repose sur l'existence de bases orthonormées. Une base 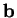 de
de  est orthonormée pour le produit scalaire
est orthonormée pour le produit scalaire 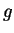 si
si
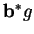 est le produit scalaire canonique
de
est le produit scalaire canonique
de
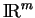 . Soient alors des produits scalaires
. Soient alors des produits scalaires 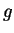 et
et 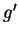 et des bases
et des bases 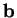 et
et 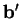 orthonormées pour
orthonormées pour 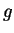 et
et 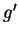 respectivement. On a
respectivement. On a
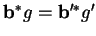 et par conséquent
et par conséquent 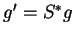 , où
, où
Cela dit, l'action (22) n'est pas libre. Les éléments du stabilisateur d'un produit scalaire 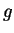 forment précisément le groupe
forment précisément le groupe 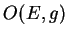 des isométries de l'espace vectoriel euclidien
des isométries de l'espace vectoriel euclidien 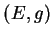 (on les appelle aussi transformations othogonales). C'est un groupe isomorphe à
(on les appelle aussi transformations othogonales). C'est un groupe isomorphe à 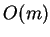 . Notons que si
. Notons que si
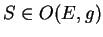 , alors
, alors
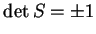 .
.




suivant: A..4.2 L'application
monter: A..4 Produits scalaires
précédent: A..4 Produits scalaires
Table des matières
![]() forment précisément le groupe
forment précisément le groupe ![]() des isométries de l'espace vectoriel euclidien
des isométries de l'espace vectoriel euclidien ![]() (on les appelle aussi transformations othogonales). C'est un groupe isomorphe à
(on les appelle aussi transformations othogonales). C'est un groupe isomorphe à ![]() . Notons que si
. Notons que si
![]() , alors
, alors
![]() .
.