



suivant: 5 Applications affines et
monter: 4 Géométrie Euclidienne
précédent: 4.4.4 Les formules d'Appolonius
Table des matières
Longueur, aire et volume sont généralement définis au moyen de l'intégrale de Lebesgue, étudiée en analyse. Pour des figures géométriques
``simples": segment de droites, triangles, parallélogrammes, pyramides, etc. elle rend des formules appartenant à la culture générale et que l'on trouve dans
toutes les bonnes encyclopédies. Nous admettrons ces formules qui seront éventuellement justifiées dans le cadre du cours d'analyse. Pour des courbes et
surfaces générales, nous reviendrons sur la question dans un chapitre ultérieur.
- La longueur d'un segment de droite
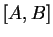 a été définie plus haut, comme la distance séparant ses extrémités.
a été définie plus haut, comme la distance séparant ses extrémités.
- L'aire d'un parallélogramme
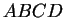 est le produit des longueurs d'un côté et de la hauteur correspondante, par exemple le côté
est le produit des longueurs d'un côté et de la hauteur correspondante, par exemple le côté
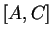 et la hauteur issue de
et la hauteur issue de 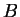 . Celle-ci valant
. Celle-ci valant
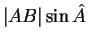 , en dimension
, en dimension 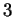 ,
l'aire du parallélogramme vaut donc
,
l'aire du parallélogramme vaut donc
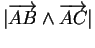 . Dans un plan Euclidien rapporté à un repère orthonormé dans lequel les composantes de
. Dans un plan Euclidien rapporté à un repère orthonormé dans lequel les composantes de
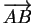 et
et
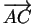 sont
sont 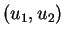 et
et 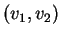 , elle est donnée par
, elle est donnée par
- Le volume d'un parallélépipède
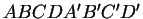 , dans lequel
, dans lequel 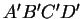 s'obtient en translatant le parallélogramme
s'obtient en translatant le parallélogramme 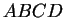 , est le produit de l'aire d'une
de ses faces par la longueur de la hauteur correspondante. En dimension
, est le produit de l'aire d'une
de ses faces par la longueur de la hauteur correspondante. En dimension 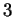 , ayant choisi une orientation arbitraire, une normale unitaire au plan de
, ayant choisi une orientation arbitraire, une normale unitaire au plan de 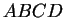 est par
exemple
La longueur de la hauteur relative à cette face est donc
Ainsi, le volume du parallélépipède est donné par
est par
exemple
La longueur de la hauteur relative à cette face est donc
Ainsi, le volume du parallélépipède est donné par
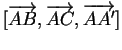 .
Dans un repère orthonormé où les composantes de
.
Dans un repère orthonormé où les composantes de
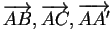 sont
sont
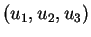 ,
,
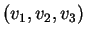 et
et
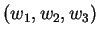 , il vaut, indé
pendamment de l'orientation choisie,
, il vaut, indé
pendamment de l'orientation choisie,




suivant: 5 Applications affines et
monter: 4 Géométrie Euclidienne
précédent: 4.4.4 Les formules d'Appolonius
Table des matières
2002-12-17
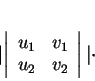
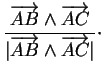
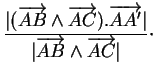
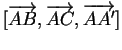 .
Dans un repère orthonormé où les composantes de
.
Dans un repère orthonormé où les composantes de
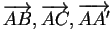 sont
sont

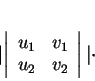
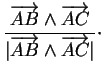
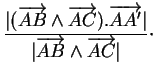
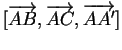 .
Dans un repère orthonormé où les composantes de
.
Dans un repère orthonormé où les composantes de
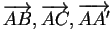 sont
sont
