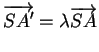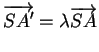suivant: 2.5.1.2 Le théorème de
monter: 2.5.1 Le théorème de
précédent: 2.5.1 Le théorème de
Table des matières
Soient un plan  et un point
et un point  ne lui appartenant pas.
Pour tout point
ne lui appartenant pas.
Pour tout point  , sauf si elle est parallèle à
, sauf si elle est parallèle à  , la droite
, la droite
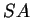 perce ce dernier en un point
perce ce dernier en un point 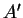 appelé projection centrale de
appelé projection centrale de  sur
sur  depuis
depuis  . Nous le noterons éventuellement
. Nous le noterons éventuellement
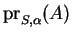 . Puisque
. Puisque 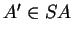 , on a toujours
pour un certain
, on a toujours
pour un certain 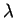 . Dans l'énoncé ci-dessous, le rapport de section est défini comme dans la Remarque 3.3.
. Dans l'énoncé ci-dessous, le rapport de section est défini comme dans la Remarque 3.3.
2002-12-17