



suivant: 5.3.1.0.1 Conservation des produits
monter: 5.3 Isométries
précédent: 5.3 Isométries
Table des matières
Une application affine
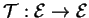 est une isométrie si elle conserve les distances, c'est-à-dire si
est une isométrie si elle conserve les distances, c'est-à-dire si
pour tous
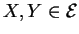 .
.
On a vu plus haut que c'est le cas des translations.
Proposition 5.3.1
Une application affine
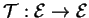
est une isométrie si et seulement si l'application linéaire
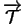
est orthogonale, c'est-à-dire conserve le produit
scalaire:
Preuve. L'application affine
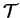 est une isométrie si et seulement si
pour tous
est une isométrie si et seulement si
pour tous
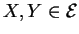 , autrement dit, si
, autrement dit, si
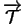 conserve la longueur de ses arguments.
conserve la longueur de ses arguments.
Si tel est le cas, alors il conserve le produit scalaire, à cause de la formule
qui exprime le produit scalaire
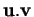 au moyen des longueurs de combinaisons
linéaires de
au moyen des longueurs de combinaisons
linéaires de
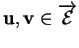 .
.
Inversement, il est évident que
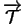 conserve les longueurs de ses arguments s'il conserve le produit scalaire.
conserve les longueurs de ses arguments s'il conserve le produit scalaire.
Corollaire 5.3.2
Une application affine est une isométrie si et seulement si, dans un repère orthonormé, elle est représentée sous la forme (
22)
où
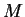
est une matrice orthogonale. En particulier, si
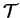
est une isométrie, alors elle est bijective et
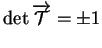
.
Preuve. En effet, la matrice représentant une application orthogonale dans une base orthonormée est orthogonale et réciproquement. De plus, le
déterminant d'une matrice orthogonale vaut 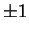 .
.
Une isométrie
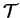 est positive ou négative selon que
est positive ou négative selon que
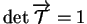 ou
ou
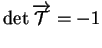 respectivement.
Par exemple, lorsque la droite
respectivement.
Par exemple, lorsque la droite
 est orthogonale à l'hyperplan
est orthogonale à l'hyperplan  , la symétrie
, la symétrie
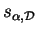 est une isométrie négative. On l'appelle la symétrie orthogonale par rapport à
est une isométrie négative. On l'appelle la symétrie orthogonale par rapport à  et on la note
et on la note 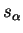 . On l'appelle encore la réflexion par rapport à
. On l'appelle encore la réflexion par rapport à  car, en dimension
car, en dimension 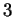 , elle
modélise la transformation d'un objet en l'image qu'en donne un miroir plan modélisé par
, elle
modélise la transformation d'un objet en l'image qu'en donne un miroir plan modélisé par  .
.
Sous-sections




suivant: 5.3.1.0.1 Conservation des produits
monter: 5.3 Isométries
précédent: 5.3 Isométries
Table des matières
2002-12-17
![]() est une isométrie si elle conserve les distances, c'est-à-dire si
est une isométrie si elle conserve les distances, c'est-à-dire si
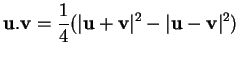
![]() conserve les longueurs de ses arguments s'il conserve le produit scalaire.
conserve les longueurs de ses arguments s'il conserve le produit scalaire.![]()
![]() est positive ou négative selon que
est positive ou négative selon que
![]() ou
ou
![]() respectivement.
Par exemple, lorsque la droite
respectivement.
Par exemple, lorsque la droite
![]() est orthogonale à l'hyperplan
est orthogonale à l'hyperplan ![]() , la symétrie
, la symétrie
![]() est une isométrie négative. On l'appelle la symétrie orthogonale par rapport à
est une isométrie négative. On l'appelle la symétrie orthogonale par rapport à ![]() et on la note
et on la note ![]() . On l'appelle encore la réflexion par rapport à
. On l'appelle encore la réflexion par rapport à ![]() car, en dimension
car, en dimension ![]() , elle
modélise la transformation d'un objet en l'image qu'en donne un miroir plan modélisé par
, elle
modélise la transformation d'un objet en l'image qu'en donne un miroir plan modélisé par ![]() .
.