

suivant: Les modules
monter: A propos des densités
précédent: Signe des densités
Il est clair que l'union des espaces
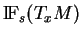 ,
, 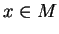 , est un fibré vectoriel au-dessus de la variété
, est un fibré vectoriel au-dessus de la variété 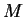 . Il est de rang
. Il est de rang 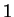 . On le note
. On le note
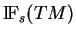 .
Si
.
Si
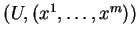 est une carte de
est une carte de 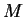 alors,
alors,
en est une trivialisation au-dessus de 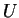 . Pour
. Pour 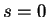 ,
,
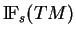 est le fibré trivial
est le fibré trivial
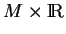 .
.
Nous noterons
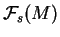 l'espace des sections
l'espace des sections
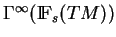 de ce fibré.
Nous les appellerons champs de
de ce fibré.
Nous les appellerons champs de 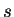 -densités, voire
-densités, voire 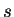 -densités ou densités si aucune confusion n'en résulte. On a
-densités ou densités si aucune confusion n'en résulte. On a
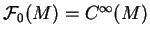 .
.
Par définition, la dérivée de Lie 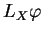 d'un champ de
d'un champ de 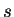 -densités
-densités 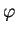 dans la direction d'un champ de vecteurs
dans la direction d'un champ de vecteurs 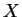 est le champ de
est le champ de 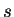 -densités
-densités
où 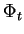 est le flot de
est le flot de 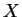 .
.
Proposition 0.2
Si, dans une carte
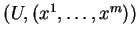
,
où
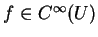
, alors
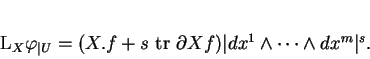 |
(1) |
Preuve. Observons que la fonction 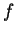 est la valeur de
est la valeur de 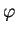 sur le champ de tenseurs
sur le champ de tenseurs
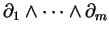 . Le coefficient de
. Le coefficient de
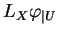 selon
selon
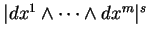 est donc la dérivée en
est donc la dérivée en 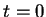 de
de
La formule annoncée en découle aussitôt si on remarque que
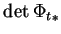 est positif pour
est positif pour 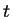 assez voisin de
assez voisin de 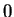 .
.
Il est à présent immédiat de vérifier que muni de la dérivée de Lie 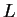 ,
,
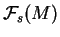 est une représentation de l'algèbre de Lie des champs de vecteurs de
est une représentation de l'algèbre de Lie des champs de vecteurs de 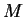 et que, de plus, si
et que, de plus, si 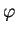 est une
est une 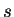 -densité et
-densité et 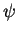 est une
est une 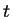 -densité, alors
-densité, alors 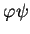 est une
est une 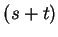 -densité et, pour tout champ de vecteurs
-densité et, pour tout champ de vecteurs 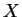 ,
,
Il suffit pour cela d'effectuer les calculs dans une carte arbitraire de 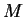 .
.
Proposition 0.3
a) Les fibrés
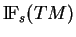
sont triviaux.
b) Le fibré
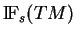
admet une section naturelle partout non nulle si et seulement si
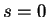
.
c) Les sections naturelles de
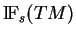
sont les fonctions constantes.
Preuve. Considérons une partition de l'unité 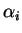 subordonnée à un recouvrement ouvert localement fini de
subordonnée à un recouvrement ouvert localement fini de 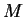 par des domaines de cartes
par des domaines de cartes 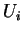 . Notons
. Notons 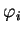 le champ de
le champ de 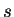 -densités
-densités
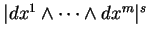 associé aux coordonnées locales définies dans
associé aux coordonnées locales définies dans 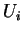 . Les densités
. Les densités
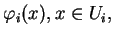 sont toutes (strictement) positives. On obtient alors un champ de
sont toutes (strictement) positives. On obtient alors un champ de 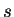 -densités
-densités
qui ne s'annule en aucun point de 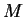 . Ceci prouve a).
. Ceci prouve a).
Supposons que les dérivées de Lie 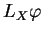 d'un champs de
d'un champs de 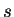 -densités
-densités 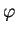 soient nulles.
La formule (1) montre que si
soient nulles.
La formule (1) montre que si
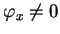 alors
alors 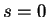 , ce qu'on voit en choisissant
, ce qu'on voit en choisissant 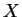 de façon que
de façon que 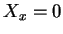 et
et
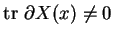 . Les points b) et c) en découlent aussitôt.
. Les points b) et c) en découlent aussitôt.


suivant: Les modules
monter: A propos des densités
précédent: Signe des densités
2002-12-17
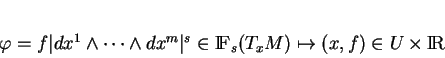
![]() l'espace des sections
l'espace des sections
![]() de ce fibré.
Nous les appellerons champs de
de ce fibré.
Nous les appellerons champs de ![]() -densités, voire
-densités, voire ![]() -densités ou densités si aucune confusion n'en résulte. On a
-densités ou densités si aucune confusion n'en résulte. On a
![]() .
.
![]() d'un champ de
d'un champ de ![]() -densités
-densités ![]() dans la direction d'un champ de vecteurs
dans la direction d'un champ de vecteurs ![]() est le champ de
est le champ de ![]() -densités
-densités
![]() ,
,
![]() est une représentation de l'algèbre de Lie des champs de vecteurs de
est une représentation de l'algèbre de Lie des champs de vecteurs de ![]() et que, de plus, si
et que, de plus, si ![]() est une
est une ![]() -densité et
-densité et ![]() est une
est une ![]() -densité, alors
-densité, alors ![]() est une
est une ![]() -densité et, pour tout champ de vecteurs
-densité et, pour tout champ de vecteurs ![]() ,
,
![]() d'un champs de
d'un champs de ![]() -densités
-densités ![]() soient nulles.
La formule (1) montre que si
soient nulles.
La formule (1) montre que si
![]() alors
alors ![]() , ce qu'on voit en choisissant
, ce qu'on voit en choisissant ![]() de façon que
de façon que ![]() et
et
![]() . Les points b) et c) en découlent aussitôt.
. Les points b) et c) en découlent aussitôt.
![]()