

suivant: La divergence
monter: A propos des densités
précédent: Le fibré des -densités
Etudions à présent les représentations
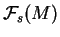 de l'algèbre de Lie
de l'algèbre de Lie 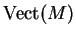 .
.
Proposition 0.4
Les
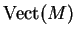
-modules
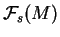
et
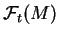
sont isomorphes si et seulement si
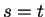
.
Preuve. On peut supposer que 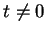 . D'après le lemme ci-dessous, un isomorphisme
. D'après le lemme ci-dessous, un isomorphisme
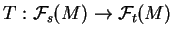 est une application locale. D'après le théorème de Peetre, c'est donc, localement, un opérateur différentiel. Nous sommes ainsi ramenés à étudier les opérateurs différentiels
est une application locale. D'après le théorème de Peetre, c'est donc, localement, un opérateur différentiel. Nous sommes ainsi ramenés à étudier les opérateurs différentiels
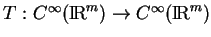 vérifiant identiquement
vérifiant identiquement
Exprimée pour des champs de vecteurs constants, cette relation montre que les coefficients de 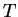 sont constants. Les champs de vecteurs du premier degré, indivergentiels, montrent que, comme polynôme en
sont constants. Les champs de vecteurs du premier degré, indivergentiels, montrent que, comme polynôme en 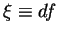 ,
, 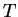 est invariant sous l'action de
est invariant sous l'action de
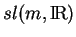 . Par conséquent,
. Par conséquent, 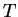 est la multiplication par une constante, non ulle,
est la multiplication par une constante, non ulle, 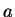 . (1) L'égalité ci-dessus se résume alors à
. (1) L'égalité ci-dessus se résume alors à
qui équivaut à 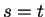 .
.
Lemme 0.5
Si
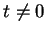
, toute application
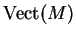
-equivariante
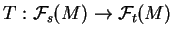
est locale.
Preuve. Soient un ouvert 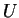 de
de 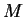 et une
et une 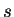 -densité
-densité 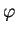 nulle dans
nulle dans 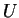 . Supposons que
. Supposons que
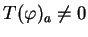 pour un certain point
pour un certain point 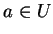 . Il existe un champ de vecteur
. Il existe un champ de vecteur 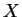 , à support compact dans
, à support compact dans 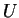 , nul en
, nul en 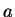 et pour lequel
et pour lequel
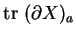 , exprimé dans des coordonnées locales au voisinage de
, exprimé dans des coordonnées locales au voisinage de 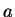 , ne soit pas nul. Autrement dit,
, ne soit pas nul. Autrement dit,
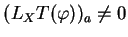 (cf. (1)). Cependant,
(cf. (1)). Cependant, 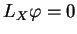 de sorte que
de sorte que
une contradiction.
Proposition 0.6
Le module
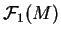
est isomorphe à
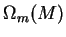
si et seulement si
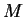
est orientable.
Preuve. Si 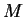 est orienté par la forme
est orienté par la forme 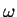 , alors
, alors 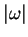 est une
est une 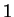 -densité de
-densité de 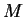 qui ne s'annule en aucun point et
qui ne s'annule en aucun point et
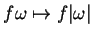 ,
,
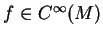 , est un isomorphisme de
, est un isomorphisme de 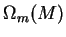 sur
sur
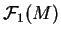 .
.
Inversement, soit 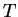 un tel isomorphisme. Une variante immédiate du lemme précédent montre que
un tel isomorphisme. Une variante immédiate du lemme précédent montre que 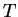 est un opérateur diffrérentiel d'ordre
est un opérateur diffrérentiel d'ordre 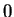 . Soit une section partout non nulle
. Soit une section partout non nulle 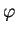 de
de
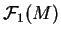 . La forme
. La forme
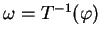 ne s'annule en aucun point de
ne s'annule en aucun point de 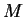 . En effet, si elle s'annulait en
. En effet, si elle s'annulait en 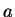 , il en irait de même de
, il en irait de même de
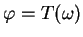 puisque
puisque 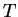 est d'ordre
est d'ordre  .
.


suivant: La divergence
monter: A propos des densités
précédent: Le fibré des -densités
2002-12-17
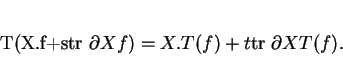
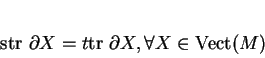
![]() un tel isomorphisme. Une variante immédiate du lemme précédent montre que
un tel isomorphisme. Une variante immédiate du lemme précédent montre que ![]() est un opérateur diffrérentiel d'ordre
est un opérateur diffrérentiel d'ordre ![]() . Soit une section partout non nulle
. Soit une section partout non nulle ![]() de
de
![]() . La forme
. La forme
![]() ne s'annule en aucun point de
ne s'annule en aucun point de ![]() . En effet, si elle s'annulait en
. En effet, si elle s'annulait en ![]() , il en irait de même de
, il en irait de même de
![]() puisque
puisque ![]() est d'ordre
est d'ordre ![]() .
.
![]()