



suivant: A..4 Produits scalaires
monter: A..3 Densités
précédent: A..3.1 Définition
Table des matières
Il est évident que le produit de densités est encore une densité, dont le poids est la somme des poids des facteurs. Dans le même ordre d'idées, les densités ont un signe et on peut élever une densité positive à n'importe quelle puissance. En effet, si la valeur d'une densité est positive (nulle ou négative) en une base de  , alors ses valeurs sur les autres bases sont également positives (respectivement nulles ou négatives). Nous dirons donc qu'une densité
, alors ses valeurs sur les autres bases sont également positives (respectivement nulles ou négatives). Nous dirons donc qu'une densité  est positive ou négative selon que
est positive ou négative selon que
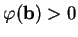 ou
ou
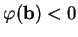 pour un
pour un
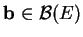 , sachant qu'alors ses valeurs sont toutes du signe en question.
, sachant qu'alors ses valeurs sont toutes du signe en question.
Il est clair que si  est une
est une 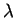 -densité positive, alors pour tout
-densité positive, alors pour tout
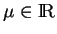 ,
,
est une densité positive de poids
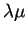 . Cette observation permet de décrire toutes les densités à partir d'une seule densité
. Cette observation permet de décrire toutes les densités à partir d'une seule densité 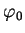 positive de poids
positive de poids  car
car
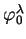 est alors une base de
est alors une base de
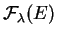 .
.
![]() est une
est une ![]() -densité positive, alors pour tout
-densité positive, alors pour tout
![]() ,
,