A.2.2 Action de sur les bases de

suivant: A..3 Densités monter: A..2 Bases d'un espace précédent: A..2.1 Définition Table des matières

A.2.2 Action de $% latex2html id marker 22756 $ GL(m,{\rm I\!R})$$ sur les bases de

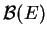Nous noterons ${\mathcal B}(E)$ l'ensemble des bases de

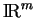. L'ensemble des bases de $% latex2html id marker 22764 $ {\rm I\!R}^m$$ n'est autre que l'ensemble des bijections linéaires de 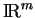$% latex2html id marker 22766 $ {\rm I\!R}^m$$ sur lui-même. C'est donc un groupe pour la composition des applications. Il est d'habitude désigné par 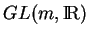$% latex2html id marker 22768 $ GL(m,{\rm I\!R})$$ et on note 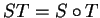$ST=S\circ T$ sa multiplication. L'ensemble 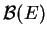${\mathcal B}(E)$ n'est pas un groupe. 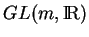Par contre, $% latex2html id marker 22774 $ GL(m,{\rm I\!R})$$ opère dessus à droite par l'action

$% latex2html id marker 22776 $\displaystyle ({\bf b},S)\mapsto {\bf b}.S:={\bf b}\circ S $$

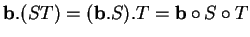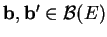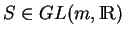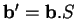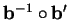En effet, $% latex2html id marker 22778 $ {\bf b}.(ST)=({\bf b}.S).T={\bf b}\circ S\circ T$$ . De plus, cette action est transitive et libre car si $% latex2html id marker 22780 $ {\bf b},{\bf b}'\in{\mathcal B}(E)$$ , alors il existe un unique $% latex2html id marker 22782 $ S\in GL(m,{\rm I\!R})$$ pour lequel $% latex2html id marker 22784 $ {\bf b}'={\bf b}.S$$ , à savoir $% latex2html id marker 22786 $ {\bf b}^{-1}\circ{\bf b}'$$ .