

suivant: À propos de ce
monter: A propos des densités
précédent: La divergence
Notons  une dérivée covariante de
une dérivée covariante de 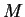 , de torsion nulle. On lui associe l'application
, de torsion nulle. On lui associe l'application
On voit facilement qu'en coordonnées locales,
les 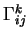 étant les symboles de Christoffel de
étant les symboles de Christoffel de  .
.
Proposition 0.11
a) Il existe une
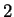
-forme différentielle fermée
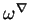
de
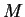
telle que
b) Si

est la dérivation covariante associée à la connexion de Levi-Civita d'une métrique riemannienne de
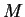
, alors
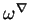
est nul et
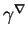
est une divergence de
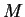
.
c) La classe de cohomologie de de Rham de
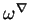
est indépendante de

et donc nulle.
Preuve. Le point a) résulte immédiatement de l'expression de 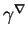 en coordonnées locales. On remarquera d'ailleurs que la forme
en coordonnées locales. On remarquera d'ailleurs que la forme 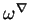 s'exprime à l'aide de la courbure de
s'exprime à l'aide de la courbure de  par la formule
par la formule
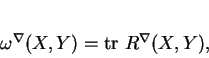 |
(2) |
ce qu'on voit avec un peu de calcul.
Le point c) résulte de b) et de ce que la différence entre deux dérivations covariantes (de torsion nulle) 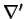 et
et  est de la forme
est de la forme
où 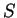 est un tenseurs de type
est un tenseurs de type 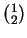 , symétrique. Si on note
, symétrique. Si on note 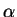 la
la 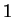 -forme
-forme 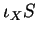 de
de 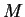 , alors
, alors
Enfin, le point b) résulte de la formule (2) et du fait que la courbure de la connexion de Levi-Civita est à valeurs dans les applications antisymétriques, dont la trace est nulle.
En conclusion, on voit qu'une dérivation covariante donne un opérateur différentiel qui est une divergence quand elle est associée à une métrique riemannienne et qui peut être corrigée par une 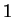 -forme pour devenir une divergence dans le cas général.
-forme pour devenir une divergence dans le cas général.
Remarquons par ailleurs que, si 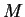 est orienté par une forme
est orienté par une forme 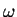 , on construit une divergence par la formule
, on construit une divergence par la formule
Celle-ci n'est autre que la restriction de la codifférentielle aux tenseurs de degré 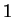 .
.


suivant: À propos de ce
monter: A propos des densités
précédent: La divergence
2002-12-17
![]() une dérivée covariante de
une dérivée covariante de ![]() , de torsion nulle. On lui associe l'application
, de torsion nulle. On lui associe l'application
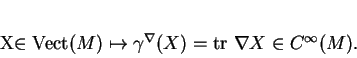
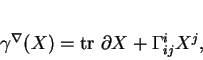
![]() -forme pour devenir une divergence dans le cas général.
-forme pour devenir une divergence dans le cas général.
![]() est orienté par une forme
est orienté par une forme ![]() , on construit une divergence par la formule
, on construit une divergence par la formule