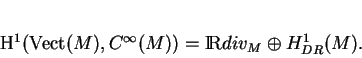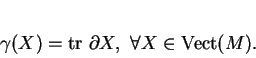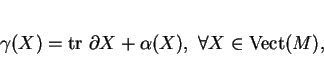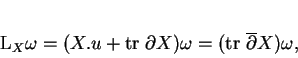

suivant: Divergence et connexion
monter: A propos des densités
précédent: Les modules
Le fait que les modules
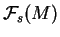 ne soient pas isomorphes se traduit par l'existence d'une classe de cohomologie non nulle de
ne soient pas isomorphes se traduit par l'existence d'une classe de cohomologie non nulle de 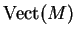 à coefficients dans
à coefficients dans 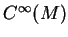 . On l'obtient en considérant que
. On l'obtient en considérant que
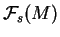 est une déformation de
est une déformation de
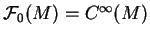 .
.
Fixons une section sans zéro 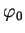 de
de
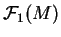 , à valeurs non négatives (2). On en déduit une section sans zéro
, à valeurs non négatives (2). On en déduit une section sans zéro
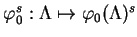 de
de
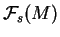 et une bijection
et une bijection
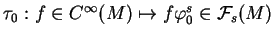 .
.
Proposition 0.7
a)Il existe un
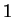
-cocycle
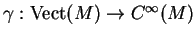
tels que
b)L'application
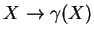
est un opérateur différentiel de symbole
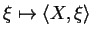
.
c) La classe de cohomologie de
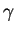
est indépendante de
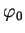
.
Preuve. Dans une carte
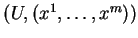 de
de 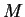 , on a
, on a
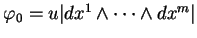 , où la fonction
, où la fonction 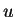 est partout positive sur
est partout positive sur 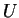 . Dans cet ouvert, on a donc
. Dans cet ouvert, on a donc
Ceci démontre a) et b). Pour c), on constate que si on remplace 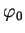 par
par 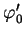 , alors
, alors 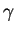 est remplacé par
est remplacé par
La classe de cohomologie 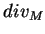 de
de 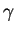 s'appelle la classe de la divergence. Un quelconque de ses représentants pouvant s'appeler une divergence. Pour rappel,
s'appelle la classe de la divergence. Un quelconque de ses représentants pouvant s'appeler une divergence. Pour rappel,
Proposition 0.8
Le premier espace de cohomologie de
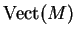
à valeurs dans
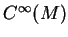
vaut
Concernant une divergence arbitraire de 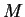 , la propriété suivante peut être utile.
, la propriété suivante peut être utile.
Proposition 0.9
Si
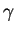
est une divergence de
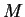
, alors il existe un atlas de
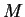
dans toute carte duquel
Preuve. D'après ce qui précède, dans toute carte
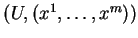 de
de 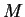 ,
,
où 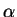 est une
est une 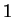 -forme fermée de
-forme fermée de 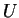 . Si celui-ci est contractile,
on peut supposer qu'elle est la différentielle d'une fonction
. Si celui-ci est contractile,
on peut supposer qu'elle est la différentielle d'une fonction 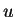 . Etant donné
. Etant donné 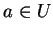 , la forme différentielle
, la forme différentielle
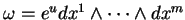 ne s'annulant en aucun point de
ne s'annulant en aucun point de 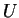 , on peut trouver des coordonnées locales
, on peut trouver des coordonnées locales 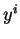 dans un voisinage de
dans un voisinage de 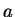 dans lesquelles (cf. le lemme ci-dessous)
dans lesquelles (cf. le lemme ci-dessous)
En calculant la dérivée de Lie 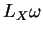 dans les deux systèmes de coordonnées, on obtient
dans les deux systèmes de coordonnées, on obtient
où 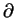 et
et
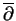 représentent les dérivées selon les
représentent les dérivées selon les 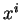 et les
et les 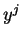 respectivement. Ainsi, dans les nouvelles coordonnées,
respectivement. Ainsi, dans les nouvelles coordonnées, 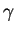 à la forme indiquée.
à la forme indiquée.
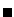
Pour être complet, nous établissons la propriété suivante, bien classique.
Lemme 0.10
Si
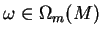
ne s'annule pas en
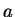
, alors il existe une carte de
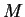
au voisinage de
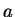
dans laquelle
Preuve. Dans une carte quelconque de 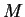 au voisinage de
au voisinage de 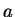 ,
, 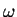 s'écrit
s'écrit
où 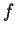 est une fonction de classe
est une fonction de classe 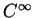 qui ne s'annule pas en
qui ne s'annule pas en 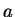 . Si
. Si 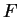 en est une primitive par rapport à
en est une primitive par rapport à 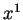 , alors
, alors
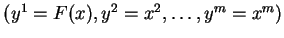 est un nouveau système de coordonnées locales de
est un nouveau système de coordonnées locales de 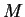 au vosinage de
au vosinage de 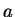 , dans lequel
, dans lequel 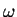 prend la forme voulue.
prend la forme voulue.

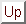

suivant: Divergence et connexion
monter: A propos des densités
précédent: Les modules
2002-12-17
![]() de
de
![]() , à valeurs non négatives (2). On en déduit une section sans zéro
, à valeurs non négatives (2). On en déduit une section sans zéro
![]() de
de
![]() et une bijection
et une bijection
![]() .
.
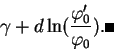
![]() de
de ![]() s'appelle la classe de la divergence. Un quelconque de ses représentants pouvant s'appeler une divergence. Pour rappel,
s'appelle la classe de la divergence. Un quelconque de ses représentants pouvant s'appeler une divergence. Pour rappel,