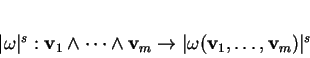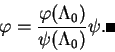

suivant: Signe des densités
monter: A propos des densités
précédent: Introduction
Une 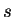 -densité sur un espace vectoriel
-densité sur un espace vectoriel 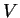 de dimension finie
de dimension finie 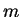 est une application
est une application
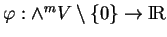 qui est homogène de poids
qui est homogène de poids 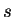 , c'est-à-dire telle que
, c'est-à-dire telle que
pour tout
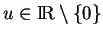 et tout
et tout
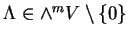 .
L'ensemble de ces applications est visiblement un espace vectoriel, sous-espace de l'espace des applications de
.
L'ensemble de ces applications est visiblement un espace vectoriel, sous-espace de l'espace des applications de
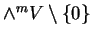 dans
dans 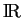 . On le note
. On le note
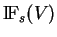 . Lorsque
. Lorsque 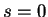 , c'est
, c'est 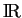 .
.
Proposition 0.1
L'espace
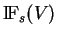
est de dimension
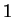
.
Si
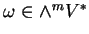
n'est pas nul, alors
en est une base.
Preuve. Il est clair que 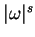 est une
est une 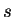 -densité sur
-densité sur 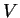 . Par ailleurs, si
. Par ailleurs, si 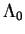 est une base de
est une base de 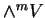 , alors, pour toute
, alors, pour toute 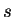 -densités
-densités 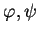 sur
sur 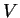 , il est évident que
, il est évident que
Sous-sections
2002-12-17