



suivant: 3.2.2 Longueur et angle
monter: 3.2 Produit scalaire, longueur
précédent: 3.2 Produit scalaire, longueur
Table des matières
Un produit scalaire de  est une loi qui à deux éléments
est une loi qui à deux éléments 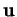 et
et 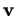 de
de  associe un nombre
associe un nombre
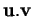 ayant les propriétés suivantes:
ayant les propriétés suivantes:
-
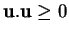 , l'égalité ayant lieu si et seulement si
, l'égalité ayant lieu si et seulement si
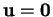
-
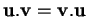
-
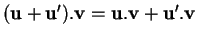 ,
,
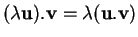
où
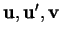 sont quelconques dans
sont quelconques dans  et où
et où 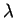 est un nombre réel arbitraire.
La dernière propriété exprime le fait que le produit scalaire est linéaire en son facteur de gauche; à cause de la seconde, il l'est également à droite.
Le carré scalaire
est un nombre réel arbitraire.
La dernière propriété exprime le fait que le produit scalaire est linéaire en son facteur de gauche; à cause de la seconde, il l'est également à droite.
Le carré scalaire
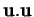 est parfois noté
est parfois noté 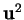 .
.
Un espace vectoriel Euclidien est un espace vectoriel muni d'un produit scalaire.
Exemple 3.2.1
Dans
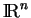
, l'application définie par
est un produit scalaire.
Les vérifications sont immédiates. Ce produit scalaire est le produit canonique de
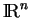 .
.
Dans la suite de cette section,  est muni d'un produit scalaire.
est muni d'un produit scalaire.
2002-12-17
![]() .
.
![]() est muni d'un produit scalaire.
est muni d'un produit scalaire.